You Too Can Physics! A 65 Foot Ant-Man Should Weigh How Much?

So – that new Ant-Man and the Wasp trailer, huh?

Particularly, that part where Scott (Ant-Man) Lang brags to Bill Foster (the former Goliath) that the largest he’d ever grown was 65 feet to Foster’s 21. Hope (Evangeline Lilly) van Dyne shuts the men down in an appropriate fashion, as you can image.

65 feet. That’s big. If you go by the ballpark idea that one story of a building in about 10 feet, than Ant-Man could’ve easily looked in a sixth storey window. If we mix our summer action movie properties, Ant-Man would tower over Jurassic World’s 20’ tall T. rex, and even look down on Indominus Rex which stands 45’ tall. Or, to put it graphically…

That’s pretty tall. So yeah – Star Lord could just call Ant-Man to help him fix his problems in…oh…yeah.

For the Love of Pym Particles

Okay look – before we get rolling, yes, Ant-Man gets really really small and really really big via Pym Particles, and thank God for that. Without that little bit of Marvel Science Magic, there’s just no way. So – before it starts, I have come here to praise Pym Particles, not bury them. In doing so, I want to explain why you need a workaround for the 65-foot claim, and what life would be like without it.

Pym Particles first appeared in 1962’s Tales to Astonish #27, and have become one of the cornerstone technologies (up there with things like Reed Richards’ unstable molecules, Tony Stark’s repulsor tech, and Professor Xavier’s Cerebro) of the Marvel Universe. They were, of course, discovered by Dr. Henry  Pym, and are still seen as subatomic particles that could alter the mass and size of living matter. Marvel’s Pym Particles followed just behind Dr. Ray Palmer’s white dwarf star matter at DC Comics that allowed him to become that company’s microscopic hero, the Atom (1961).

In recent years and amid readers with increasing scientific knowledge, Marvel writers have works to attach some science to Pym Particles with varying levels of success. One of the best attempts was by Ryan North, writer of The Unbeatable Squirrel-Girl. In issue #14  (you can grab the issue online at Comixology.com here) – guest-starring Scott Lang, and the tiny hero explained it as:

They adjust the Planck constant, the Higgs field and the space between atoms while also shunting matter between here and a place called “the Kosmos dimension.” It’s all very scientific. Uh, allegedly.

Later in the issue, North actually flashed back to a physics lecture Squirrel-Girl attended, where the professor spoke about the square cube law and Pym particles:

If I could, just for a second here, comic book writers, please use what North did here as a reason to include more physics lecture snippets in your stories. 

Got that? Quite simply and elegantly, North carved Pym Particles and cosmic rays their own scientific space in the Marvel Universe. If you just grow – without the hand-wavey science protection offered by Pym Particles or cosmic rays – you have to pay the square-cube law’s price. If you’re a Pym Particle-powered hero (or villain) or use cosmic rays, the yet-undiscovered science of those two particles somehow protects you. Like it does for Ant-Man. 

Good enough for me.

So why do you need protection from the square-cube law?

Thought you’d never ask.

Paying the Piper: Getting Big Without Pym Particles

I’ve written about this before, talking about Kong, but it’s always worth a second look. The square-cube law is something that gets drilled into physics students when they reach a certain level that often, when you see it mentioned, it’s mentioned in a context of, “everyone knows about this, so I’m not going to take the time to explain it here…”

But that leaves a lot of people behind. Not Ant-Man, mind you – but a lot. 

So let’s get in on the ground floor and explain this so that you – yes, you – can do one of these problems at any time. They’re simple. Seriously. I’m not just saying that because I’m one of those people who’s had the square-cube law drilled into me.

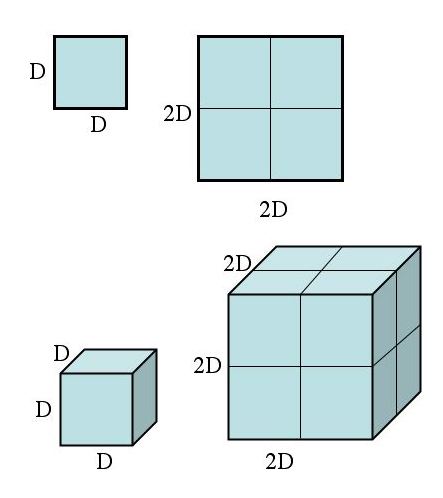
The big picture of the square-cube law is that when you’re talking about growing something (or shrinking something, but that’s for another time), the surface area of the thing increases by the square of your multiplier (how many times larger the new version is compared to the old version), and the volume of the thing increases by the cube of the multiplier. Volume is the space taken up by a thing, and that space is filled with mass, so it’s safe to say that that the weight of the thing that got bigger increases by the cube as well.

As I talked about back with Kong, this is easy to visualize if you think about squares and then make cubes.

Think of it like this – or do this. Cut out a square of paper, with each side being two inches. The area of the square is length x width, or 2 x 2 = 4 in². Simple stuff, right?

Now, double the sides of your square so they’re 4 inches instead of 2. The area of the square? 4 x 4 = 16 in². You doubled the length of the sides (2 inches to 4 inches), but your surface area increased by a factor of four (4 in² to 16 in²), or in other words, the new surface area is proportional to the square of the multiplier. Your multiplier was 2 (doubling the length), so the new surface area went up by the square of 2, 4. The original area was 4 in², and 4 multiplied by 2² = 16 in². This holds true if you triple the length (36 in²), quadruple it (64 in²) and on and on and on.

For the volume, take your square and make it a cube. Start with your original one – 2 inches per side. The volume of a regularly shaped object is its length x height x width, so in this case, 2 x 2 x 2 = 8 in³. Double the side of your cube on each side so it’s 4 inches on each side. The volume of your cube, which is just twice as big as your original, is 4 x 4 x 4 = 64 in³. Like with the surface area, let’s look at the multiplier – 2 (you doubled all the sides), so the new volume was the cube of the multiplier, 8 (2³ = 8). The original volume was 8 in³, and 8 x 2³ = 64 in³. Again, this continues if you triple the sides of your original cube (216 in³), quadruple it (512 in³), and on and on and on.

In short – double anything’s height, you’ve increased its surface area by a factor of 4, and its insides by a factor of 8. Or as the cool kids say, the surface area increases by the square, the volume increases by the cube.

Simple, Simple Math

Mathematically, the two parts of the square-cube law look like this:

A₂ = A₁ (l₂/l₁)²

Where l1 is the original length (or height), l2 is the new length, A1 is the original surface area, and A2 is the new surface area, and

V₂ = V₁ (l₂/l₁)³

Where V1 is the original volume, and V2 is the new volume.

All you have to do in order to figure out how much a 65-foot Ant-Man would weigh (on our earth, not in the Marvel Universe where the Pym Particles protect him) is divide his final height by his original height. In Scott’s case, that’s 65 feet (780 inches) divided by 5’10” (70 inches – actor Paul Rudd’s real height).

That’s 11.1 – let’s just round that to 11. That’s your multiplier.

Another way to say it is that Ant-Man’s height at 65 feet is 11 times that of his normal height.

Scott’s surface area increases by the square of that multiplier, so if we were worried about Scott’s surface area – which we aren’t, but there are big implications (again, if he were in our universe) in terms of heat loss, he would have 11^2 times the surface area at 65 feet than he did at 5’10”.

The heat loss alone is a huge, huge issue, but we’re not going into that now.

Let’s talk volume and weight. Our multiplier for the 65’ Ant-Man is 11, so Scott’s volume is increased by 11³ (11 x 11 x 11). That volume is filled by his mass, which isn’t the same as, but yet swappable for weight, so Scott’s weight at 65’ would be:

Scott’s assumed weight: 180 lbs

180 lbs x 11³ = 239,580 lbs.

That’s right around 120 tons. That’s a blue whale’s worth of weight.

And that’s a lot.

Our World Says No

There’s a reason blue whales live in water. Their weight is in part supported by the water that surrounds them. Take them out of water, and they rapidly die – for any number of reasons, but chief among them is that their body cannot support the weight of their organs and connective tissue. No, just because humans aren’t whales doesn’t make it all better.  

Structurally, something that has the shape and proportions of a human being cannot weight 239,580 pounds – without the protection of Pym Particles.

Elephants look the way they do because their legs – their big, fat legs have a larger cross-sectional area than human legs do. You will never see an elephant with skinny legs, no matter how hard you look or how long you live. The strength of a column (or leg) is directly proportional to the cross-sectional area. The thicker the leg, the more weight it can support.

And that’s just the start of the problems a human-sized thing that’s 65 feet tall (and unprotected by Pym Particles) would have. For more, check out the Kong article. The structure of human beings can support life at the scale of average human beings. Get too much bigger, and structurally-related health problems start (that goes for getting smaller too) – unless you’re protected by Pym Particles.

Back to The Unbeatable Squirrel-Girl, issue #14’s bad guy, Enigmo learns this the hard way. Able to control his mass and size (and apparently not blessed with an overabundance of intelligence), Enigmo opts to fight a giant iron Man action figure (you should really read the story) by growing to the same scale as the embiggened figure.

Immediately, his fibula breaks. No Pym Particles of cosmic rays, there.

I’m a STEM Teacher – What Can I do With This?

I’ve said it before, I teach IB Physics, but that shouldn’t mean that anything I do is un-scaleable or impossible for other STEM students. The week the new trailer showing Lang and Foster…”comparing sizes” came out, this was my offer for some extra credit on the test they recently took:

And that’s it. Nothing else. They needed to find the relationship, do any conversions they felt necessary, and report an answer. Those that attempt it shouldn’t have much of a problem with it, and probably some will cite my Kong article. Okay – maybe I should’ve thought this through some more.

But as for use in the classroom, go ahead and show the trailer. It’s for a PG-13 movie though, so please be aware of that. Use the students’ heightened engagement to get a discussion going – not the “how could you…” which leads to a dead end, but rather the, “what happens when…” which is open-ended and allows students to use what they know to explain a clearly impossible situation.

Guide the discussion, of course, and bring it all around to the square-cube law. As with the physics professor shown above from The Unbeatable Squirrel-Girl, ask your students why a mouse looks like a mouse, and an elephant looks like an elephant, rather than just a giant mouse. Once they have the idea, then bring in the math.

Get a weight, and then start to talk about what this might mean for a living human being. Take it back to the mouse vs. elephant idea. Should a giant human look like a normal human, but just really big?

And of course, bring in the Pym Particles at the end as the “magic science” of the Marvel Universe – because without them…let’s not even consider. Thank God for Pym Particles.