Skyscraper’s Leap of Physics: Is Dwayne Johnson Superhuman?

There’s something about the just-released poster for Skyscraper.

Okay, full-on admission: I love Dwayne Johnson, and I have an unholy, good taste-defying love for all of his projects, from his wrestling days as The Rock through G.I. Joe to Moana and Jumanji to this summer’s Skyscraper and his upcoming projects like Rampage and more.

Speaking of Skyscraper, let’s get some context (if the name didn’t give it away…). Johnson’s was Tweeting and Insagramming about the film as he was in active production, so you may have already seen some images of a beaten-up Johnson inside a tall building. The story is set in China (he-loo Chinese box office!) and sets Johnson up as a family man facing some…challenges. The official description for the movie reads:  

Global icon Dwayne Johnson leads the cast of Legendary’s Skyscraper as former FBI Hostage Rescue Team leader and U.S. war veteran Will Ford, who now assesses security for skyscrapers.  On assignment in China he finds the tallest, safest building in the world suddenly ablaze, and he’s been framed for it.  A wanted man on the run, Will must find those responsible, clear his name and somehow rescue his family who is trapped inside the building…above the fire line.

Okay, so the poster shows Johnson’s character, leaping from something (a crane? A ladder from a flying fire truck?) into the titular skyscraper. Okay – yes, it’s not realistic. It’s not meant to be realistic, and something in your brain when you look at that image told you that. But it’s not meant to be “right.” It’s visual hyperbole. It’s hype for the movie. That image alone tells you everything you need to know about the movie: there’s a skyscraper. Dwayne Johnson is there. And the action/stunts are going to be edge-of-your-seat insane. I fully admit it’s not meant to be taken literally.

That doesn’t mean we can’t though.

I look at that image, and I’m interested in why. Why does virtually anyone who looks at that picture think it’s either ridiculous or awesome – but not real? I doubt that very many people look at it and think that it’s remotely realistic, yet few, if any people could explain why. Heck, just looking at it, I can’t explain why. It’s not like we’ve all tried to make a leap like that before, and missed. We, as a culture…as a species…can look at that leap and somehow run some internal physics and come to a simple conclusion: nope.

I’m not going to get into the psychology of the image here, and what instinctual and primitive parts of our brain it lights up, though. What I’m going to do here is look at the real physics side of things, and get a little mathematical confirmation that that part of our brains saying, “Nope” is 100% correct.

Of Falling Fords and Horizontal Launches

To set up the analysis of this image, I need to assume a thing or two. First – that before the image, Johnson’s character, Will Ford, ran across the structure shown in the upper right. I’m also assuming that Skyscraper is set on earth, which means that the acceleration due to gravity is the standard 9.81 m/s2.

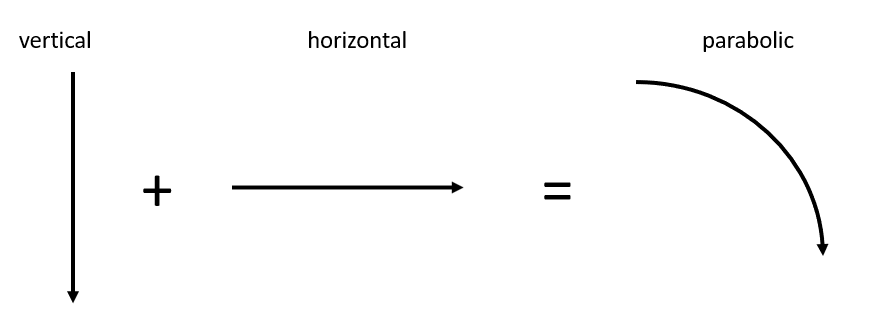
The problem type we’re looking at is projectile motion, or more specifically, a horizontal launch. It’s the same thing as firing a cannonball off of the top of a cliff. The cannonball, os in this case, Ford, will have two types of motion: horizontal and vertical.

The horizontal velocity of the projectile (again, Ford), will be constant. Well, mostly constant – air resistance would slow him down a little, but that would be minimal and we’re not going to worry about it in this analysis. The reason the velocity in the horizontal is constant is because as soon as the pushing force stops acting on the projectile (Ford), there is no force acting on it. Nope – nothing. When physics students first run into this, many will fight to try and put some kind of force or acceleration on the horizontal motion, but as they analyze it further, they realize there’s nothing there. Nothing (aside from maybe some minimal air resistance if it’s a short trip) is pushing (or slowing) that projectile.

The vertical velocity of the horizontally-launched projectile is easy to analyze and calculate. It’s just something that’s in free fall. The specifics of this mean that the only force acting on the object once the pushing force stops acting on it (from the launch) is gravity, and that’s pulling it straight down. There’s your acceleration.  

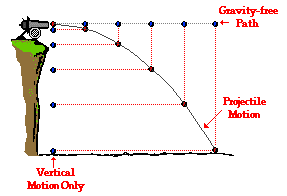
So again, a horizontally-launched projectile is a combination of two motions, horizontal (out) and vertical (down). The thing that links the two velocities together is time. Both of their motions have to work in the same amount of time. That means that if we can calculate how long it takes the projectile to reach the ground (or other level in this example), that time is the same time it takes the projectile to go “out” horizontally. Add those two motions together, and the object’s motion tracks out half a parabola.

Or with a cartoon, via The Physics Classroom: 

If you’re like many physics students, part of your brain is fighting this. But it’s true. This is the reason why those cool steel bearing launches at science museums work the way they do, and it’s also why – as Jamie and Adam showed on Mythbusters – if you fire a bullet out of a gun and drop a bullet at the exact same millisecond the fired bullet leaves the barrel, they will take exactly the same amount of time to reach the ground. One will just be way further away.

How Far Does Ford Fall?

The key to figuring out the plausibility of the whole image lies in figuring out some distances – specifically, the sides of a triangle. A right triangle. The Pythagorean Theorem will be making an appearance shortly.

I’m going to assume this image was taken straight-on, in the same plane as the action and environmental pieces, which makes measurements easier. The only thing in the image that I can scale from is Johnson in mid-air. Johnson is, despite occasional claims to the contrary, a normal human being, so his proportions should be those of a normal human. I’ll just look up Johnson’s height, and…holy crap, he’s 6’5”! Okay – maybe he’s more than human…

Back to scaling: the image is very clear, and his leg position is very easy to mimic. I tried it and got about 1.1 meters, but I’m only 6’. Let’s add another .2 meters on just to be on the safe side here, and call the distance from his front toe to his back toe 1.3 meters.

This is our real measurement, and the measurement by which we scale the distances in the image. If you have access to image analysis software, you can just set the distances and make your measurements. If not, a ruler is your friend. Personally, I used Vernier’s LoggerPro3, because I use is in school and have it on my computer.

The sides of my triangle I’m interested in are the c and b of the Pythagorean Theorem, with c being the hypotenuse (the diagonal in the image). I need to use the Pythagorean Theorem to solve for the distance between the two endpoints of those sides – or the drop that Ford is hoping to make in order to get into the skyscraper, rather than be a free falling projectile (which is a whole other problem).

Rounding, I’m using 9.8 m for b and 11.0 m for c, so running that through

a^2 + b^2 = c^2

I get a value of 5.0 meters for a. That means, according to my calculation, the target Ford needs to hit is 5 meters below his launch point. I like the value. Why? A normal story of a building is about 3 meters, and the distance between the two sides of the triangle covers a little more than one story. I’m good with my distance.

Time is the Enemy

As I mentioned before, and in this case, Ford’s horizontal motion is locked to his vertical motion by time. The time it takes for him to drop from the crane arm to the floor by the broken window is all the time he has to get across the distance between the crane and the building. Be sure you’ve got that – there is zero wiggle room.

And you always fall faster than you think.

What’s Ford’s time budget? We can calculate that with the free fall formula, a modified piece of the general kinematics formulas of physics:

y = 1/2gt^2

Where:

y = vertical displacement (in meters – 5 m for our calculation)

g = gravity, 9.81 m/s2

t = time (in seconds)

Rearrange to solve for time and you get:

t = sqrt(2y/g)

Plugging the numbers in, I got a time of 1 second.

That’s it. As far as Ford would be concerned in the scene that the image shows, 1 second is all the time in the world. That’s it – zero wiggle room.

That means that he has one second to cover the horizontal distance of 9.8 meters. That’s all.  

That makes his minimal launch speed easy to calculate – he has one second to cover 9.8 meters, so he needs to leave that crane arm at 9.8 m/s. More than that – he’d be okay. Less than that, he’s got a little bit of time to think about the choices that led him to his predicament of the ground rushing to meet him.

Just to sum up – as soon as ford leaps, gravity starts tugging him down at a rate of 9.8 meters/second every second. Thanks to his horizontal launch speed, he’s still moving horizontally across the distance, but he’s still going down. He has one second to cover that distance and make the edge of that target window.

And no, if the crane was higher up, that wouldn’t have helped. Given enough time, gravity’s pull on Ford will turn his trajectory into a pure vertical fall. The longer he has to fall, the more of his horizontal distance he’s going to lose.

What if the crane was angled more, say pointing directly into the window? It might help a little, but gravity is always a harsh mistress, and she’s going to bend you to her will, not the other way around.

So – the most likely outcome of the jump, as Facebook user Phillip Michael Ballesteros Sr. skillfully Photoshopped:

But Maybe He Can…  

Okay – I mentioned it earlier, Johnson (and by extension Ford) is possibly super-human. Running across something that’s basically a horizontal ladder may be something he can do at 9.8 m/s. Let’s look at where that would put him with other humans…

Since Johnson used to play football, what about NFL players? A speed of 9.8 m/s would put him way ahead of Bo Jackson who covered 40 yards (36.6 meters) in a verified 4.12 seconds at an NFL Combine in 1986. That’s about 8.88 m/s.

Usain Bolt’s world record time for the 100 meter dash was 9.58 seconds, which comes out to 10.44 m/s.

And if we come around the other side and look at world records for long jumps (the distance of which would be, in part a function of velocity at launch), things still fall a little short – the current world record is held by American Olympian Mike Powell who, in 1991, hit a distance of 8.95 m at the Tokyo Olympics.

Hey – maybe adrenaline fueled a burst of speed for Johnson, and he was able to make the leap.

Or maybe he is super human.

How Can I Use this in my STEM Classroom?

There’s no disguising it – this is a straight-up projectile motion problem. My thoughts on using this in my classes are 1) I hope my students aren’t reading this right now, and 2) Pretty much just like I explained above. If you have access to photo analysis software let students work with a digital version, but if not – rulers and scales. I’d prefer that, and if my students end up with this as a problem, that’s what they’ll get.

Give it a go, and see what they do with it.