How much power would it take to cook Wolverine to his skeleton?
With Wolverine back among the living in the Marvel Universe (as of Marvel Legacy), we thought it would be a good time to look at one of Wolverine’s more notable “deaths.”
Yeah…Wolverine has a thing about dying. He’s done it a lot. There have been a few “canon” Marvel Universe Wolverine deaths (the latest included) where he gets better thanks to his healing factor, and there have been a ton of them in alternate timelines and What If? stories.
It’s one of those alternate timeline stories that we’re looking at here: Uncanny X-Men #141-142 from 1981. “The Days of Future Past” storyline. If your only experience with the X-Men and something called “Days of Future Past” is the 2014 movie, you owe it to yourself to check out the source material. In it, Kitty Pryde, to stop a horrific future from unfolding for mutants in the United States, travels from a dystopian future where mutants are hunted by Sentinels to the past to inhabit the mind of her younger self. While the X-Men work in the present, the surviving X-Men of the future battle Sentinels. In what’s becoming a legendary scene, Colossus picks up Wolverine and throws him at a Sentinel in what they call the “fastball special.” The unsurprised Sentinel turns and blasts Wolverine with an energy ray, vaporizing his body, leaving only his adamantium skeleton behind.
That description right there does grave injustice to the storyline, and again, if you’ve never read it, you really, really need to. You can pick it up in trade form at your local comic shop, or digitally at Comixlogy, right here)
So what’s to get all sciencey over?
Let’s figure out how much power it would take to vaporize a Wolverine and some other stuff.
First things first, along with our assumptions:
By power, we’re talking about:
Power = energy/time
And the energy source is the blast coming from the Sentinel – which we’re going to assume is heat energy, therefore our equations are:
Q = mcΔT
Where:
Q = heat energy, measured in Joules (1 food Calorie = 4184 Joules)
m = the mass of the object being heated, in this case Wolverine…or the fleshy bits of Wolverine, as we’ll see in a minute
c = the specific heat capacity of the thing being heated, or how much heat is needed to change the 1 kg of the material (Wolverine) by 1°C
ΔT = the change in temperature of the material (Wolverine)
And:
Q = mL
Where:
L = the latent heat of vaporization – how much energy is needed, per kg of material (Wolverine) to turn him from a liquid to a vapor.
As for assumptions, we’re going to assume that Wolverine is mostly water – or at least the fleshy part of Wolverine is mostly water, which is reasonable. According to Marvel.com’s database of characters, Wolverine weighs in at 300 lbs., of which, 105 lbs. of that is his adamantium skeleton, leaving 195 of human tissue. Converting that to kilograms, we get that 195 lbs. is about 88.5 kg. That’s the mass of what we’ll be heating up.
Also – we’ll assume that Wolverine is running at a normal human body temperature, 37°C, when he begins his ill-fated attack.
Finally, we’ll assume that the Sentinel hit Wolverine with the blast for 3 seconds. It’s not that short, and it’s not that long – it hits a nice sweet spot that carries the idea of both power and menace on the part of the Sentinel.
As always, if you’ve got any problems with the assumptions we’re making, use your own numbers and run the math the same way.
In order the attack this problem, let’s think about what Wolverine must do. Going with the assumption that he’s water, we need to warm that water up from 37° to 100°C to vaporize it. When Waterverine is 100°C, the Sentinel needs to keep the heat up to turn that 88.5 kg of water into 88.5 kg of vapor (Steamverine?) All of that must be done in 3 seconds.
Three parts to this problem then:
- Heat Waterverine up to 100°C
- Turn Waterverine into Steamverine
- Figure out how much power the Sentinel needed to do the above in 3 seconds.
Let’s get cooking.
Part One: Heating Up Waterverine
Students new to physics or chemistry (two places where you can run into this kind of problem) always think this type of problem is far more complicated than it is. It really isn’t. To figure out how much energy is needed to warm a given mass of water up a set temperature, all you have to do is multiply the mass of the water by the specific heat capacity of the water by the difference between your starting temperature and your final temperature. It’s super easy.
Q = mcΔT, right? Okay – mass is 88.5 kg, c is easily looked up as 4,190 J/kg °C, and ΔT is 100° – 37° = 63°.
[Side note – the specific heat capacity’s units? J/kg °C? That just means that it takes 4,190 Joules per kilogram of water to increase its temperature by 1°C. If you feel we’re assuming too much saying that Wolverine is water, then plug in a different c for a different material, steak, chicken, etc.]
Let’s do the math:
Q = (88.5)(4,190)(63)
Q = 2.32 x 107 J
That’s a lot of heat – a lot of energy. But that’s expected. Waterverine has a fair amount of mass, and water takes a lot of energy to get its temperature moving. Think about putting a big pot of water on the stove to boil. Takes a while to get going, right?
Part Two: Turning Waterverine into Steamverine
If you thought the last step was easy, just wait – this one is easier still.
All we have to do here is multiply the mass (88.5 kg) by the latent heat of vaporization for water, which any reference table will tell you is 2.256 x 106 J/kg °C. That’s it.
So:
Q = mL
Q = (88.5)(2.256 x 106)
Q = 2.00 x 108 J
Again – that’s a lot of heat, but again – it’s a lot of water that the Sentinel is turning into a lot of steam.
[The above two calculations assume that the Sentinel would stop when Waterverine just turned into Steamverine, in other words, at 100°C. If that’s not working for you, and maybe, you think, the Sentinel headed that steam up to more than 100°C, that’s fine. Just use Q = mcΔT to determine how much energy was needed. Use c = 1996 J/kg °C for the specific heat of steam, and re-calculate ΔT to match whatever your new final temperature is, and add that value on to your total, above.]
Part Three: Power Up
Again, like the previous, this is a simple calculation. Power is equal to the amount of energy delivered over time, so all we have to do is add our heats from steps one and two, and then divide them by the time in which the energy was delivered, or:
Qtotal = 2.32 x 107 J + 2.00 x 108 J
Qtotal = 2.23 x 108 J
So then, power:
Power = 2.23 x 108 Joules/3 seconds
Power = 7.44 x 107 Watts
Power is measured in Watts, where 1 Watt = 1 J/1 second. And yes, 1000 Watts = a kilowatt, and yes, the number of kilowatts used in an hour is a kilowatt-hour, which is the “unit” by which your electric company charges you for electricity. More on that later.
[Think the Sentinel did it in less than 3 seconds? Reduce the 3 to 2 or 1, and watch your Power increase. Longer cook times will decrease the Power needed.]
Putting the total power needed to vaporize Wolverine into a more manageable frame, 1 million watts = 1 Megawatt, so to vaporize Wolverine in 3 seconds, the Sentinel used 74 Megawatts.
Okay, there’s no getting around it – that sounds like a lot of power.
How much?
Megawatts are the units that are used to describe the energy requirements of a city.
For example, a typical coal-fired power plant can produce 600 MW. Facebook’s Prineville, OR datacenter uses 28 MW at peak usage. Nimitz-class nuclear warships have reactors that produce 194 MW. At peak consumption, CERN uses 200 MW. It’s suggested that 45 MW can supply a small city of about 80,000 homes.
Yeah – that’s a lot of power.
But the Sentinel only needed it for about three seconds.
So it’s not all that much – only a burst.
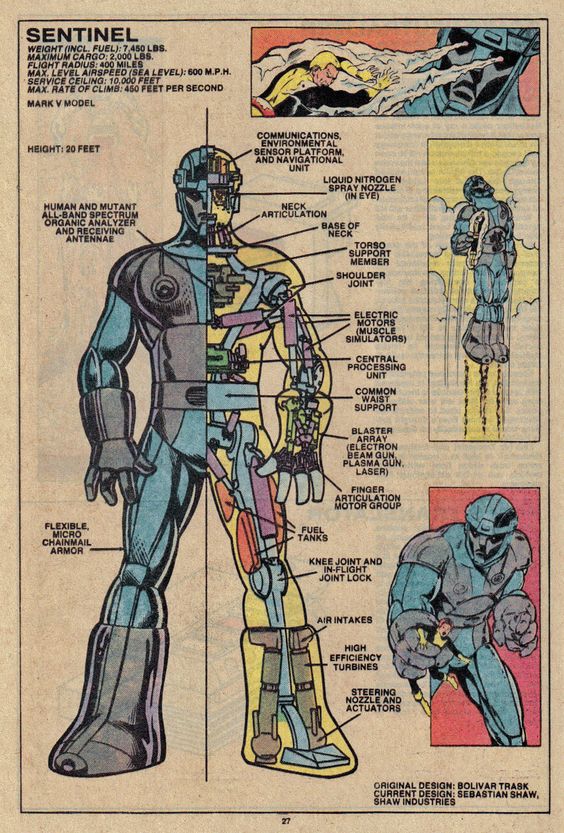
A Sentinel from the same era. Marvel played the power source close to the vest. Note the “fuel tanks” in the leg. (c) Marvel
What Fuels a Sentinel?
To make things simple, let’s assume the Sentinel, which was operating in the far future of 2013 (“Days of Future Past” was published in 1981…) had the same access to Wolverine’s data that we did, and knew that he was 88.5 kg of tissue, and thus, 74 MW for three seconds would be enough to do the job. A small power plant would run a continuous output of 74 MW, but the Sentinel only needed a three-second burst.
This, of course, leads us to the question of what kind of fuel could the Sentinel have used to produce that much power? Now we’re talking about the specific energy of a fuel – how much energy (in Joules) you can get per kilogram of that fuel. The specific energy of a fuel varies quite a bit, from about 32.5 MJ/kg for coal to 9.0 x 107 MJ/kg for Uranium-235. The difference in the specific energy of coal and uranium, for example, is why a coal-fired power plant needs, basically, mountains of coal to produce a modest 30.0 MW (at 25% efficiency), while a nuclear power plant only needs 42 kg of U-235 to produce the same.
How do we figure out how much fuel the Sentinel would need? Let’s assume 100% efficiency, that is, the Sentinel is getting every Joule of energy that the fuel source has to offer, without any waste (which is a bonkers idea, but we’ll go with it to make it simple…).
How much energy does the Sentinel need to cook Wolverine? Now 74 MW – that’s Power, or energy delivered over time. A Watt is equal to a Joule/second, so 74 MW = 74 MJ/second. The Sentinel blasted Wolverine for three seconds. So…
Energy needed = (74 MJ/second)(3 seconds)
Energy needed = 222 MJ
Coal has an energy density of 32.5 MJ/kg, so dividing the two…
Coal needed = 222 MJ/(32.5 MJ/kg)
Coal needed = 6.83 kg
Not bad. About 15 pounds of coal – if all its energy was turned into the energy needed to cook Wolverine– which it wouldn’t be.
Even Sentinels Must Pay the Energy Piper
No matter what mechanism the Sentinel uses to get the energy out of the fuel it’s using, it must obey the 2nd Law of Thermodynamics, which says that you’ll lose energy at each step. Let’s say that the Sentinel’s fuel-energy conversion mechanism, whatever it is, operates at a flat 75% efficiency – wildly improbable, but again, this was the far-flung future of 2013.
Anything less than 100% efficiency is going to up the total amount of fuel needed in our case. How can we figure out how much coal (for example) the Sentinel would need to produce 74 MW of energy at 75% efficiency?
We go to the formula:
Efficiency = energy output/energy input
Change our 75% back into a decimal, and plug in out 74 MW as our energy output. Using algebra to rearrange our formula:
Energy input = energy output/efficiency
Energy input = 74 MW/.75
Energy input = 98.7 MW
In other words, to release 74 MW of energy through a process that runs at 75% efficiency, the Sentinel would have to produce 98.7 MW of energy.
[As always, play with the numbers – believe that the Sentinels have a much better efficiency? No problem – replace the 75% with a number more to your liking and math your socks off…]
So now – let’s re-calculate how much coal the Sentinel would need to cook Wolverine. Instead of a flat 74 MW, it needs to produce 98.7 MW, which is 98.7 MJ/second for three seconds, which means the Sentinel needs to produce 291.1 MJ. Coal’s specific energy is 32.5 MJ/kg, so now…
Coal needed = 291.1 MJ/(32.5 MJ/kg)
Coal needed = 9.0 kg
Not a huge increase, but now we’re up to 19.8 pounds of coal to do the deed.
Keeping that same efficiency, how much U-235 would the Sentinel need? Just replace the coal’s specific energy with that of Uranium-235, and we’re good to go:
Uranium-235 needed = 291.1 MJ/(9.0 x 107 MJ/kg)
U-235 needed = 0.000003 kg
That’s the energy obtained from 3 milligrams of U-235 through a process operating at 75% efficiency. Big difference from coal, huh?
In terms of rough numbers, you can do the same calculation to figure out how much of other fuels the Sentinel would need to vaporize Wolverine. All you need is their specific energy. For instance:
Gasoline: 46.9 MJ/kg
Sugar: 17.0 MJ/kg
Cow Dung: 15.5 MJ/kg
That’s Cool, But Can You Explain it in Twinkies?
 And then this leads us to the fun stuff that you’ve probably seen before – figuring out how much of a “weird” fuel something would need to produce the energy that it produces. Given the above calculations this is pretty easy. In honor of Dr. Egon Spengler, let’s consider a Twinkie.
And then this leads us to the fun stuff that you’ve probably seen before – figuring out how much of a “weird” fuel something would need to produce the energy that it produces. Given the above calculations this is pretty easy. In honor of Dr. Egon Spengler, let’s consider a Twinkie.
A single Twinkie contains 135 Calories (when talking about food, a capital “C” Calorie is kilocalorie, or 1,000 small “c” calories), and 1 kilocalorie = 4184 Joules. So, by multiplying, 135 Calories = 564,840 Joules of energy.
The mass of 1 Twinkie is 38.5 grams or (divide grams by 1000 to get kilograms) 0.0385 kg.
The specific energy of a Twinkie is 564,840 J/.0385 kg = 1.47 x 107 J/kg or 14.7 MJ/kg, which puts it in the same neighborhood as sugar and cow dung according to our earlier values.
Make of that what you will.
Now – just do the same calculations as we’ve done a couple times before:
Twinkie mass needed = 291.1 MJ/(14.7 MJ/kg)
Twinkie mass needed = 19.8 kg
To quote a certain Winston Zeddemore – that’s a big Twinkie. Or a lot of Twinkies.
What About the Sentinel’s Power Bill?
There’s one last thing we can calculate when we’re talking about cooking Wolverine – how much it would cost in 2013 dollars. As mentioned earlier, consumers are charged for electricity in units of kilowatt hours (kWh).
Let’s say, for this part of the discussion, that the Sentinel is plugged in, and just draws 74 MW straight from ConEdison (the story took place in New York). What’s going to be the damage in dollars and cents?
First up, a familiar one – let’s get MW back into our Joules: 222 MJ (we’re not producing the energy here, so the efficiency isn’t an issue, and we’re going to assume that all the energy drawn as electricity is turned into heat, which…it’s not, but let’s just go with the idea here).
Now, let’s turn one kilowatt hour into Joules as well.
1 kilowatt = 1000 Joules/second, right? A kilowatt hour is therefore 1000 Joules/second for one hour.
One hour = (60 minutes)(60 seconds) = 3600 seconds.
So the number of Joules in a kilowatt hour = (1000 Joules/second)(3600 seconds) = 3.6 x 106 J or 3.6 MJ.
Got that? 1 kWh = 3.6 MJ. So – 222 MJ/3.6 MJ = 61.7, or 61.7 kWh.
How much does a kWh of electricity cost?
Rates for ConEdison in 2013 were a reported 26.99 cents per kWh.
The Sentinel needed 61.7 kWh worth of electricity to cook Wolverine.
(61.7 kWh)(26.99 cents/kWh) = 1665.28 cents, or…
$16.65.
Mutant life is cheap.
I Teach Physics/Physical Science/Chemistry. What Can I do With This?
The above problem is very similar to a variety of problems I’ve used in my physics and chemistry classes over the years. I’ve had students calculate how much energy would be needed to melt Marshmallow from Frozen, how much heat Bobby Drake gives off when he turns into Iceman (and what that would do to Colossus, if he had happened to be standing beside him), and most recently, how much power would be needed to vaporize someone with a phaser in Star Trek.
The pop culture references and engaging imagery that can go along with a problem like this will help students’ interest level from the very first look to the final explanation, either written, or in front of classmates. Most often, I require students to draw out a heating curve with the parts of the curve that correspond to parts of the problem identified.
So pick and choose from the above. Make it easier or harder, depending on your students and depth of content. Include Wolverine’s adamantium skeleton in the mix. Come up with a novel fuel source, or better yet – come up with your own new problem that hooks and engages your students.













